Introduction to Autocorrelation Times¶
Background¶
As of v1.3.0 there are two additional new convergence criterion in addition to maxGR and minTz used to evaluate whether or not the MCMC chains are converged/well-mixed. MinAfactor and maxArchange both rely on the autocorrelation time. While a more in-depth explanation of autocorrelation and its relation to convergence can be found in the documentation for emcee, we will provide a brief description here. The original RadVel convergence checks are also still in place and are described in Fulton et al. (2018).
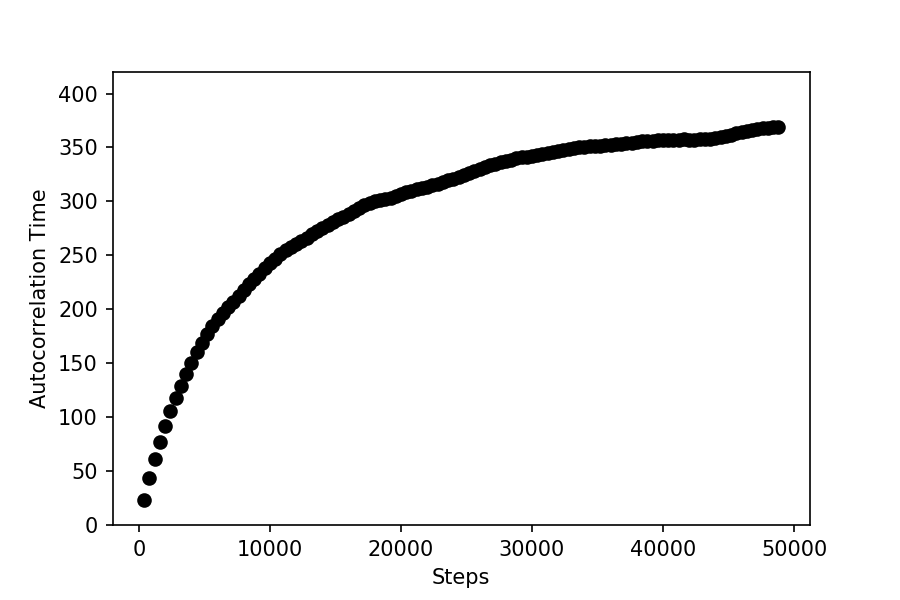
Autocorrelation time is the number of steps the walker needs to take for the chain to “forget” its initial position.
Therefore, it can be used to reduce the error in your MCMC run and to tell if it is well-mixed. Using emcee3, we can
estimate this value for each parameter in an ensemble; if multiple ensembles are run, we combine their chains to receive
the autocorrelation times.
As the chain progresses, the estimated value of the autocorrelation time (τ) becomes more accurate. In the plot below, you can see that the the estimated autocorrelation time quickly rises and then begins to plateau as it nears the true value.
minAfactor¶
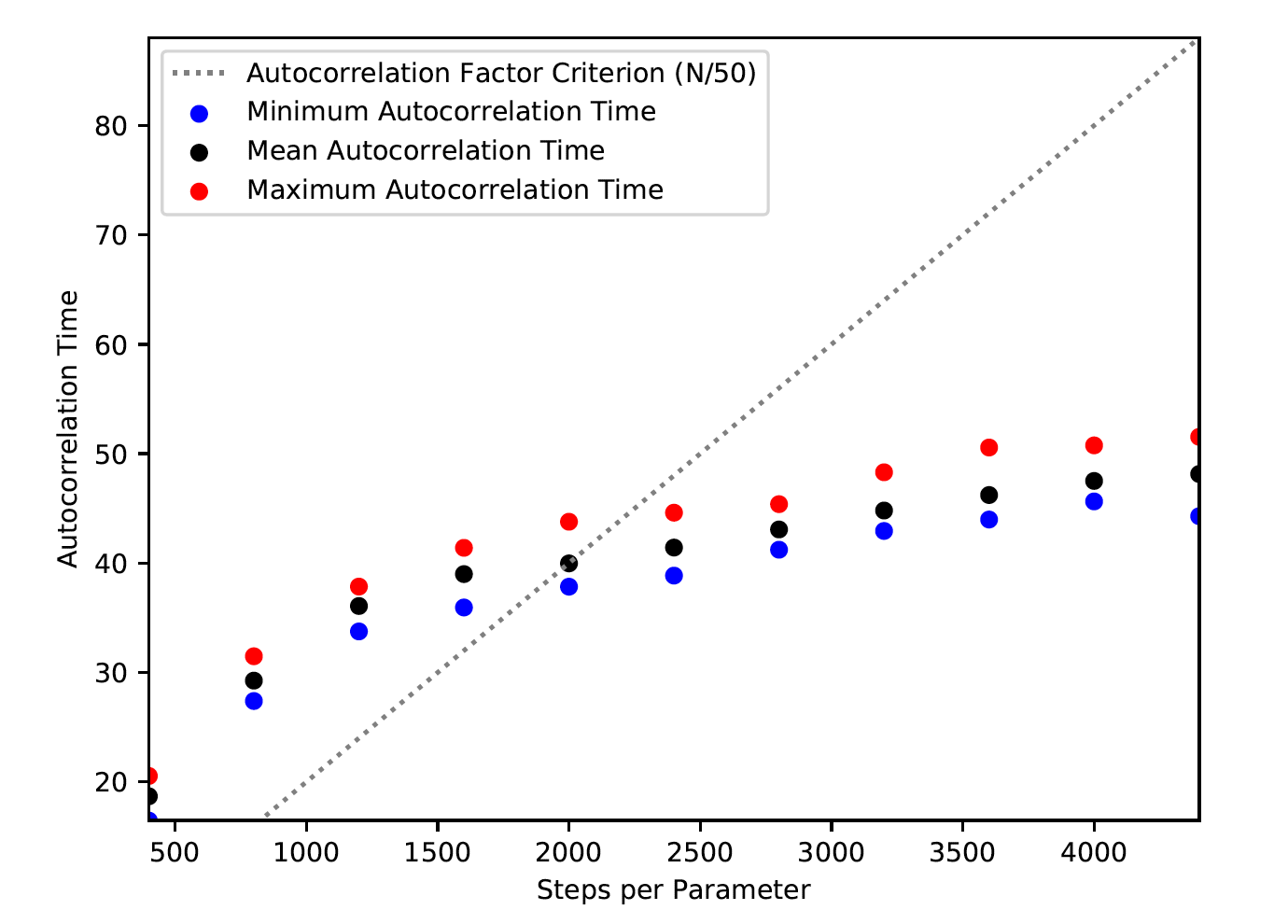
The autocorrelation time can be used to evaluate whether or not a chain is sufficiently long to be considered well-mixed. Therefore, if N steps have been
taken, N/τ ≥ c, where c is what we call the autocorrelation factor. The minimum autocorrelation factor to consider the
chains converged is represented by the criterion minAfactor. The default value for minAfactor is 40, however we find
that higher values may be useful, particularly for shorter runs; alternate values can be specified
using the minAfactor argument when calling the MCMC.
The autocorrelation factor is calculated for each parameter and the minimum of these values
is returned in real time as the MCMC run progresses.
Once the minimum autocorrelation factor is above minAfactor, this criterion
for convergence is met. Whether or not minAfactor has been satisfied can be seen in the autocorrelation plot below. Once the
maximum autocorrelation time has passed the dashed line labeled ‘Autocorrelation Factor Criterion,’ the chain is likely converged. After five consecutive status checks appear past the dashed line, the MCMC will halt if all other criterion have also been met.
maxArchange¶
While we want the autocorrelation factor to be sufficiently large, we want to make sure that it is being calculated with
an accurate estimate of the autocorrelation time. We know our estimate for τ is accurate once it begins to plateau,
allowing us to use the relative change in the autocorrelation time to infer whether or not the estimate is reliable.
We calculate the relative change in autocorrelation time for each parameter between every convergence check. The largest
of these values is also returned in real time and for the chain to be considered converged, it must fall below the
criterion maxArchange.
The default value for maxArchange is .03, where we consider the autocorrelation time to be leveling off. Rarely should
you need to increase the maxArchange argument when running radvel mcmc, but for more conservative criterion, you may
want to decrease it, particularly for long chains with large autocorrelation times (in such cases, the relative change
may be smaller, but τ has not reached its plateau).