Gaussian Process Fitting¶
by Sarah Blunt
Prerequisites¶
This tutorial assumes knowledge of the basic radvel API for \(\chi^2\) likelihood fitting. As such, please complete the following before beginning this tutorial: - radvel/docs/tutorials/164922_Fitting+MCMC.ipynb - radvel/docs/tutorials/K2-24_Fitting+MCMC.ipynb
This tutorial also assumes knowledge of Gaussian Processes (GPs) as applied to radial velocity (RV) timeseries modeling. Grunblatt et al. (2015) and Rajpaul et al. (2015) contain excellent introductions to this topic. Also check out “Gaussian Processes for Machine Learning,” by Rasmussen & Williams, a free online textbook hosted at gaussianprocesses.org.
Objectives¶
Using the K2-131 (EPIC-228732031) dataset published in Dai et al. (2017), I will show how to: - perform a maximum a posteriori (MAP) fit using a quasi-periodic kernel GP regression to model stellar activity (with data from multiple telescopes) - do an MCMC exploration of the corresponding parameter space (with data from multiple telescopes)
Tutorial¶
Do some preliminary imports:
[1]:
import numpy as np
import pandas as pd
import os
import radvel
import radvel.likelihood
from radvel.plot import orbit_plots, mcmc_plots
from scipy import optimize
%matplotlib inline
Read in RV data from Dai et al. (2017):
[2]:
data = pd.read_csv(os.path.join(radvel.DATADIR,'k2-131.txt'), sep=' ')
t = np.array(data.time)
vel = np.array(data.mnvel)
errvel = np.array(data.errvel)
tel = np.array(data.tel)
telgrps = data.groupby('tel').groups
instnames = telgrps.keys()
We’ll use a quasi-periodic covariance kernel in this fit. An element in the covariance matrix, \(C_{ij}\) is defined as follows:
Several other kernels are implemented in radvel. The code for all kernels lives in radvel/gp.py. Check out that file if you’d like to implement a new kernel.
Side Note: to see a list of all implemented kernels and examples of possible names for their associated hyperparameters…
[3]:
print(radvel.gp.KERNELS)
{'SqExp': ['gp_length', 'gp_amp'], 'Per': ['gp_per', 'gp_length', 'gp_amp'], 'QuasiPer': ['gp_per', 'gp_perlength', 'gp_explength', 'gp_amp'], 'Celerite': ['gp_B', 'gp_C', 'gp_L', 'gp_Prot']}
Define the GP hyperparameters we will use in our fit:
[4]:
hnames = [
'gp_amp', # eta_1; GP variability amplitude
'gp_explength', # eta_2; GP non-periodic characteristic length
'gp_per', # eta_3; GP variability period
'gp_perlength', # eta_4; GP periodic characteristic length
]
Define some numbers (derived from photometry) that we will use in our priors on the GP hyperparameters:
[5]:
gp_explength_mean = 9.5*np.sqrt(2.) # sqrt(2)*tau in Dai+ 2017 [days]
gp_explength_unc = 1.0*np.sqrt(2.)
gp_perlength_mean = np.sqrt(1./(2.*3.32)) # sqrt(1/(2*gamma)) in Dai+ 2017
gp_perlength_unc = 0.019
gp_per_mean = 9.64 # T_bar in Dai+ 2017 [days]
gp_per_unc = 0.12
Porb = 0.3693038 # orbital period [days]
Porb_unc = 0.0000091
Tc = 2457582.9360 # [BJD]
Tc_unc = 0.0011
Dai et al. (2017) derive the above from photometry (see sect 7.2.1). I’m currently working on implementing joint modeling of RVs & photometry and RVs & activity indicators in radvel, so stay tuned if you’d like to use those features!
Initialize radvel.Parameters object:
[6]:
nplanets=1
params = radvel.Parameters(nplanets,basis='per tc secosw sesinw k')
Set initial guesses for each fitting parameter:
[7]:
params['per1'] = radvel.Parameter(value=Porb)
params['tc1'] = radvel.Parameter(value=Tc)
params['sesinw1'] = radvel.Parameter(value=0.,vary=False) # fix eccentricity = 0
params['secosw1'] = radvel.Parameter(value=0.,vary=False)
params['k1'] = radvel.Parameter(value=6.55)
params['dvdt'] = radvel.Parameter(value=0.,vary=False)
params['curv'] = radvel.Parameter(value=0.,vary=False)
Set initial guesses for GP hyperparameters:
[8]:
params['gp_amp'] = radvel.Parameter(value=25.0)
params['gp_explength'] = radvel.Parameter(value=gp_explength_mean)
params['gp_per'] = radvel.Parameter(value=gp_per_mean)
params['gp_perlength'] = radvel.Parameter(value=gp_perlength_mean)
Instantiate a radvel.model.RVmodel object, with radvel.Parameters object as attribute:
[9]:
gpmodel = radvel.model.RVModel(params)
Initialize radvel.likelihood.GPLikelihood objects (one for each telescope):
[10]:
jit_guesses = {'harps-n':0.5, 'pfs':5.0}
likes = []
def initialize(tel_suffix):
# Instantiate a separate likelihood object for each instrument.
# Each likelihood must use the same radvel.RVModel object.
indices = telgrps[tel_suffix]
like = radvel.likelihood.GPLikelihood(gpmodel, t[indices], vel[indices],
errvel[indices], hnames, suffix='_'+tel_suffix,
kernel_name="QuasiPer"
)
# Add in instrument parameters
like.params['gamma_'+tel_suffix] = radvel.Parameter(value=np.mean(vel[indices]), vary=False, linear=True)
like.params['jit_'+tel_suffix] = radvel.Parameter(value=jit_guesses[tel_suffix], vary=True)
likes.append(like)
for tel in instnames:
initialize(tel)
Instantiate a radvel.likelihood.CompositeLikelihood object that has both GP likelihoods as attributes:
[11]:
gplike = radvel.likelihood.CompositeLikelihood(likes)
Instantiate a radvel.Posterior object:
[12]:
gppost = radvel.posterior.Posterior(gplike)
Add in priors (see Dai et al. 2017 section 7.2):
[13]:
gppost.priors += [radvel.prior.Gaussian('per1', Porb, Porb_unc)]
gppost.priors += [radvel.prior.Gaussian('tc1', Tc, Tc_unc)]
gppost.priors += [radvel.prior.Jeffreys('k1', 0.01, 10.)] # min and max for Jeffrey's priors estimated by Sarah
gppost.priors += [radvel.prior.Jeffreys('gp_amp', 0.01, 100.)]
gppost.priors += [radvel.prior.Jeffreys('jit_pfs', 0.01, 10.)]
gppost.priors += [radvel.prior.Jeffreys('jit_harps-n', 0.01,10.)]
gppost.priors += [radvel.prior.Gaussian('gp_explength', gp_explength_mean, gp_explength_unc)]
gppost.priors += [radvel.prior.Gaussian('gp_per', gp_per_mean, gp_per_unc)]
gppost.priors += [radvel.prior.Gaussian('gp_perlength', gp_perlength_mean, gp_perlength_unc)]
Note: our prior on 'gp_perlength' isn’t equivalent to the one Dai et al. (2017) use because our formulations of the quasi-periodic kernel are slightly different. The results aren’t really affected.
Do a MAP fit:
[14]:
res = optimize.minimize(
gppost.neglogprob_array, gppost.get_vary_params(), method='Nelder-Mead',
options=dict(maxiter=200, maxfev=100000, xatol=1e-8)
)
print(gppost)
parameter value vary
per1 0.369302 True
tc1 2.45758e+06 True
secosw1 0 False
sesinw1 0 False
k1 6.71302 True
dvdt 0 False
curv 0 False
gp_amp 23.3362 True
gp_explength 13.3721 True
gp_per 9.62823 True
gp_perlength 0.381962 True
gamma_harps-n -6695.13 False
jit_harps-n 0.5 False
gamma_pfs 1.66129 False
jit_pfs 5 False
Priors
------
Gaussian prior on per1, mu=0.3693038, sigma=9.1e-06
Gaussian prior on tc1, mu=2457582.936, sigma=0.0011
Jeffrey's prior on k1, min=0.01, max=10.0
Jeffrey's prior on gp_amp, min=0.01, max=100.0
Jeffrey's prior on jit_pfs, min=0.01, max=10.0
Jeffrey's prior on jit_harps-n, min=0.01, max=10.0
Gaussian prior on gp_explength, mu=13.435028842544403, sigma=1.4142135623730951
Gaussian prior on gp_per, mu=9.64, sigma=0.12
Gaussian prior on gp_perlength, mu=0.38807526285316646, sigma=0.019
Explore the parameter space with MCMC:
[15]:
chains = radvel.mcmc(gppost,nrun=100,ensembles=3,savename='rawchains.h5')
15000/15000 (100.0%) steps complete; Running 1231.70 steps/s; Mean acceptance rate = 45.7%; Min Auto Factor = 12; Max Auto Relative-Change = 0.978; Min Tz = 248.2; Max G-R = 1.012
Discarding burn-in now that the chains are marginally well-mixed
MCMC: WARNING: chains did not pass convergence tests. They are likely not well-mixed.
Note: for reliable results, run MCMC until the chains have converged. For this example, nrun=10000 should do the trick, but that would take a minute or two, and I won’t presume to take up that much of your time with this tutorial.
Make some nice plots:
[16]:
# try switching some of these (optional) keywords to "True" to see what they do!
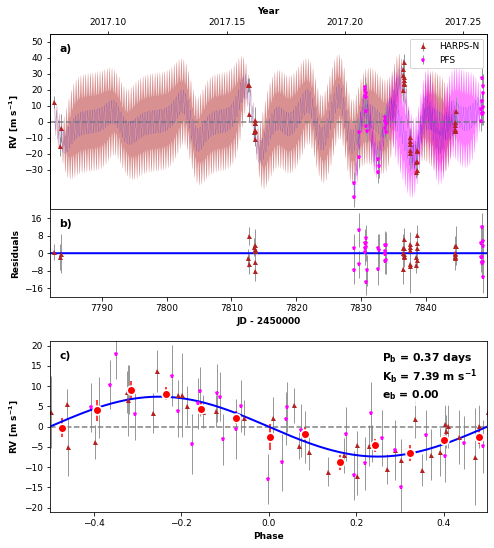
GPPlot = orbit_plots.GPMultipanelPlot(
gppost,
subtract_gp_mean_model=False,
plot_likelihoods_separately=False,
subtract_orbit_model=False
)
GPPlot.plot_multipanel()
[17]:
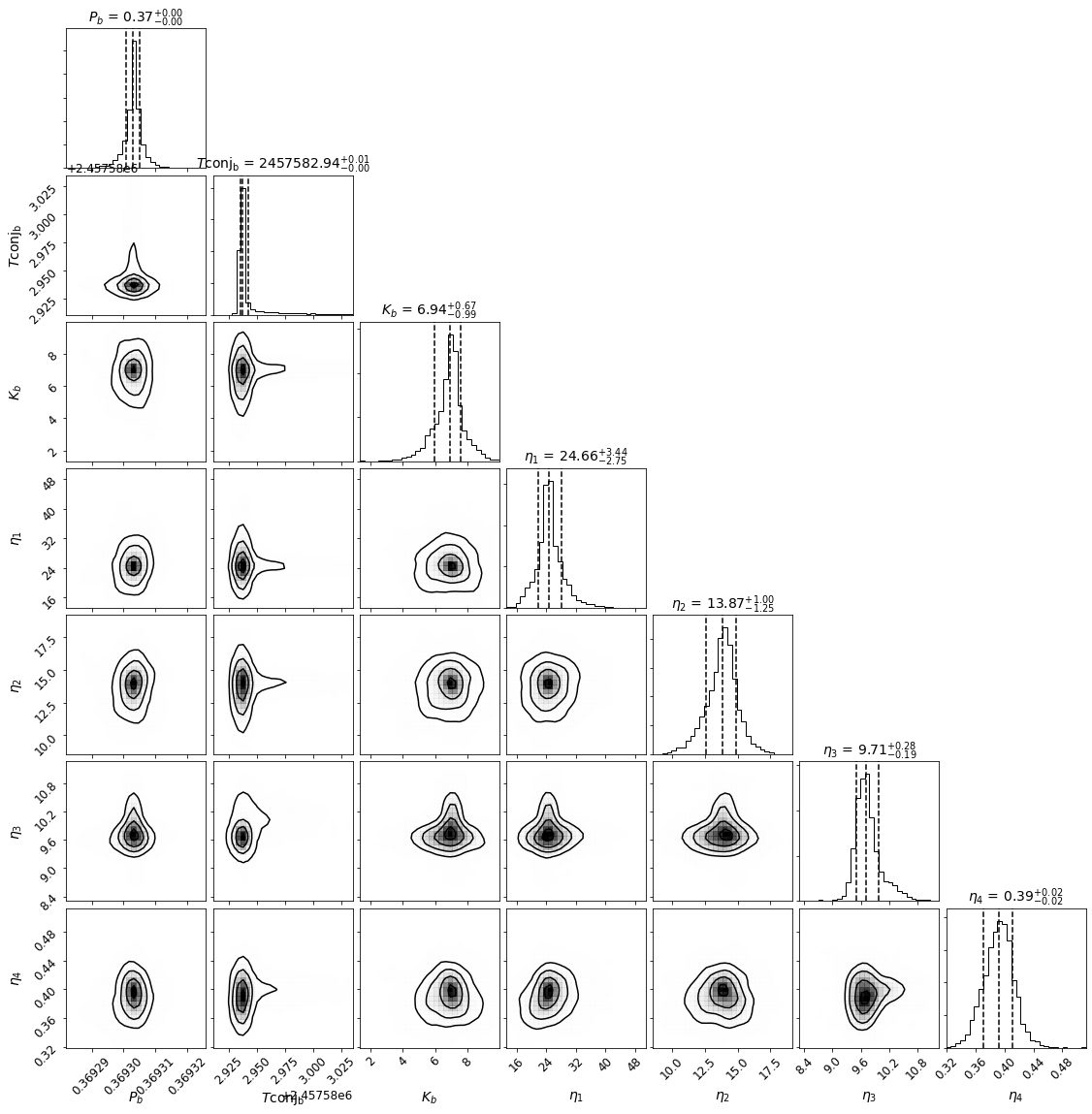
Corner = mcmc_plots.CornerPlot(gppost, chains) # posterior distributions
Corner.plot()
[18]:
quants = chains.quantile([0.159, 0.5, 0.841]) # median & 1sigma limits of posterior distributions
for par in gppost.params.keys():
if gppost.params[par].vary:
med = quants[par][0.5]
high = quants[par][0.841] - med
low = med - quants[par][0.159]
err = np.mean([high,low])
err = radvel.utils.round_sig(err)
med, err, errhigh = radvel.utils.sigfig(med, err)
print('{} : {} +/- {}'.format(par, med, err))
per1 : 0.3693031 +/- 2.1e-06
tc1 : 2457582.9366 +/- 0.0036
k1 : 6.94 +/- 0.83
gp_amp : 24.7 +/- 3.1
gp_explength : 13.9 +/- 1.1
gp_per : 9.71 +/- 0.24
gp_perlength : 0.39 +/- 0.02
Compare posterior characteristics with those of Dai et al. (2017):
per1 : 0.3693038 +/- 9.1e-06
tc1 : 2457582.936 +/- 0.0011
k1 : 6.6 +/- 1.5
gp_amp : 26.0 +/- 6.2
gp_explength : 11.6 +/- 2.3
gp_per : 9.68 +/- 0.15
gp_perlength : 0.35 +/- 0.02
gamma_harps-n : -6695 +/- 11
jit_harps-n : 2.0 +/- 1.5
gamma_pfs : -1 +/- 11
jit_pfs : 5.3 +/- 1.4
Thanks for going through this tutorial! As always, if you have any questions, feature requests, or problems, please file an issue on the radvel GitHub repo (github.com/California-Planet-Search/radvel).